DLT求解PnP问题

2023-09-05 阅读 78 评论 0

摘要：PnP问题解法问题描述 Perspective-n-Point (PnP) 问题：如下图， 1）给定 [公式] 个3D参考点 [公式] 到摄像机图像上2D投影点 [公式] 的匹配点对； 2）已知 3D点在世界坐标系下的坐标，2D点在图像坐标系下的坐标； 3）已知摄

PnP问题解法

问题描述

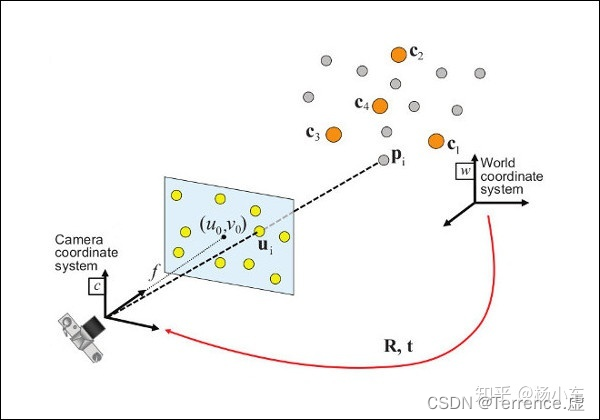
Perspective-n-Point (PnP) 问题：如下图，
1）给定 [公式] 个3D参考点 [公式] 到摄像机图像上2D投影点 [公式] 的匹配点对；
2）已知 3D点在世界坐标系下的坐标，2D点在图像坐标系下的坐标；
3）已知摄像机的内参数 [公式] 。
目的：求世界坐标系与摄像机坐标系之间的位姿变换 [公式]
用途：相机位姿跟踪，物体位姿跟踪，AR/VR，机器人操作，SLAM中位姿初值求解……
常用解法：DLT，P3P，EPnP，UPnP。
3D-2D问题
PnP算法分为直接发和优化法两大类，
直接法包括：P3P、 DLT 、 EPnP等等；
优化法有： LHM 、 Only pos BA 等。
在这里插入图片描述

DLT解法（直接线性变换）

理论推导部分

3D参考点在世界坐标系的齐次坐标：
$c=[xyz1]\mathbf{c}=\left[\begin{array}{l}x \\ y \\ z \\ 1\end{array}\right]$
对应的2D投影点在图像坐标系下的齐次坐标是：
$u=[uv1]\mathbf{u}=\left[\begin{array}{l}u \\ v \\ 1\end{array}\right]$
相机内参一般是已知的 slam’问题里
$K=[fxcxfycy1]\mathbf{K}=\left[\begin{array}{ccc}f_{x} & & c_{x} \\ & f_{y} & c_{y} \\ & & 1\end{array}\right]$
那么3D点到2D点投影可表示为
$λ[uv1]=[fxcxfycy1][R∣t][xyz1]\lambda\left[\begin{array}{l}u \\ v \\ 1\end{array}\right]=\left[\begin{array}{lll}f_{x} & & c_{x} \\ & f_{y} & c_{y} \\ & & 1\end{array}\right][\mathbf{R} \mid \mathbf{t}]\left[\begin{array}{c}x \\ y \\ z \\ 1\end{array}\right]$ (1)

$[R∣t][\mathbf{R} \mid \mathbf{t}]$ 是一个3x4的增广矩阵，包含了旋转和平移信息。
理论上由于 $[R][\mathbf{R}]$ 这个玩意儿就只有三个自由度，因为存在旋转矩阵的正交约束，DLT算法中先不管这个，忽略这个正交约束，按照 $[R∣t][\mathbf{R} \mid \mathbf{t}]$ 有12个未知参数 $x=[a1,⋯,a12]T\mathbf{x}=\left[a_{1}, \cdots, a_{12}\right]^{T}$ 来考虑计算。
这样，(1)式变化为：
$λ=[uv1]=[fxcxfycy1][a1a2a3a4a5a6a7a8a9a10a11a12][xyz1]\lambda=\left[\begin{array}{l}u \\ v \\ 1\end{array}\right]=\left[\begin{array}{ccc}f_{x} & & c_{x} \\ & f_{y} & c_{y} \\ & & 1\end{array}\right]\left[\begin{array}{cccc}a_{1} & a_{2} & a_{3} & a_{4} \\ a_{5} & a_{6} & a_{7} & a_{8} \\ a_{9} & a_{10} & a_{11} & a_{12}\end{array}\right]\left[\begin{array}{l}x \\ y \\ z \\ 1\end{array}\right]$ (2)
先消去第三个等式，也就是消去scale factor尺度因子 $λ\lambda$ ，
有：
${xfxa1+xcxa9+yfxa2+ycxa10+zfxa3+zcxa11+fxa4+cxa12−uxa9−uya10−uza11−ua12=0xfya5+xcya9+yfya6+ycya10+zfya7+zcya11+fya8+cya12−vxa9−vya10−vza11−va12=0\left\{\begin{array}{l}x f_{x} a_{1}+x c_{x} a_{9}+y f_{x} a_{2}+y c_{x} a_{10}+z f_{x} a_{3}+z c_{x} a_{11}+f_{x} a_{4}+c_{x} a_{12}-u x a_{9}-u y a_{10}-u z a_{11}-u a_{12}=0 \\ x f_{y} a_{5}+x c_{y} a_{9}+y f_{y} a_{6}+y c_{y} a_{10}+z f_{y} a_{7}+z c_{y} a_{11}+f_{y} a_{8}+c_{y} a_{12}-v x a_{9}-v y a_{10}-v z a_{11}-v a_{12}=0\end{array}\right.$
写成矩阵形式如下：
$[xfxyfxzfxfx0000xcx−uxycx−uyzcx−uzcx−u0000xfyyfyzfyfyxcy−vxycy−vyzcy−vzcy−v][a1a2⋮a12]=0\left[\begin{array}{cccccccccccc}x f_{x} & y f_{x} & z f_{x} & f_{x} & 0 & 0 & 0 & 0 & x c_{x}-u x & y c_{x}-u y & z c_{x}-u z & c_{x}-u \\ 0 & 0 & 0 & 0 & x f_{y} & y f_{y} & z f_{y} & f_{y} & x c_{y}-v x & y c_{y}-v y & z c_{y}-v z & c_{y}-v\end{array}\right]\left[\begin{array}{c}a_{1} \\ a_{2} \\ \vdots \\ a_{12}\end{array}\right]=0$

高翔的14讲用了简化表示
定义 $a=[a1a2a3a4a5a6a7a8a9a10a11a12]a=[\begin{array}{cccc}a_{1} & a_{2} & a_{3} & a_{4} \\ a_{5} & a_{6} & a_{7} & a_{8} \\ a_{9} & a_{10} & a_{11} & a_{12}\end{array}]$ 的三个行向量为：
$t⃗1=(a1,a2,a3,a4)T\vec t_{1}=(a_1, a_2,a_3,a_4)^{T}$
$t⃗2=(a5,a6,a7,a8)T\vec t_{2}=(a_5, a_6,a_7,a_8)^{T}$
$t⃗3=(a9,a10,a11,a12)T\vec t_{3}=(a_9, a_{10},a_{11},a_{12})^{T}$
于是又有：
$t⃗1TP−t⃗3TPu1=0,\vec t_{1}^{T}P-\vec t_{3}^{T}Pu_{1}=0 ,$
$t⃗2TP−t⃗3TPv1=0.\vec t_{2}^{T}P-\vec t_{3}^{T}Pv_{1}=0 .$

综上所述，每个特征点（3D-2D坐标对）提供了两个方程，也就是两个关于t的线性约束。
假设一共有N个特征点， $\geq 6$ 时，产生一个方程组：

$Ax=0\mathrm{Ax}=\mathbf{0}$
其中， $A\mathbf{A}$ 的大小为 $2n \times 12$ 。这个方程无法求出精确解，但是可以获得一个 $∣x∣=1|\mathbf{x}|=1$ 约束下的最小二乘解 $argmin⁡∥Ax∥2\operatorname{argmin}\|\mathbf{A x}\|^{2}$ (这部分可以参考： Ax=0求解以及MVG 教程) 。具体的，对 $A\mathbf{A}$ 进行SVD分解，可得
$[UΣV]=SVD⁡(A)[\mathbf{U} \mathbf{\Sigma} \mathbf{V}]=\operatorname{SVD}(\mathbf{A})$
$V\mathbf{V}$ 矩阵的最后一列 $x‾\overline{\mathbf{x}}$ , 便为式 (6) 的解。注意，求解的结果是没有尺度的，也就是说实际的解为
$x=βx‾\mathbf{x}=\beta \overline{\mathbf{x}}$
其中， $β\beta$ 为比例系数， $x‾=[aˉ1,⋯,aˉ12]T\overline{\mathbf{x}}=\left[\bar{a}_{1}, \cdots, \bar{a}_{12}\right]^{T}$ 。旋转部分为
$R‾=[aˉ1aˉ2aˉ3aˉ4aˉ5aˉ6aˉ7aˉ8aˉ9]\overline{\mathbf{R}}=\left[\begin{array}{lll} \bar{a}_{1} & \bar{a}_{2} & \bar{a}_{3} \\ \bar{a}_{4} & \bar{a}_{5} & \bar{a}_{6} \\ \bar{a}_{7} & \bar{a}_{8} & \bar{a}_{9} \end{array}\right]$
为带有尺度的正交矩阵，为求最优的旋转矩阵，将其进行SVD分解
$[UΣV]=SVD⁡(R‾)[\mathbf{U} \mathbf{\Sigma} \mathbf{V}]=\operatorname{SVD}(\overline{\mathbf{R}})$

最优的旋转矩阵即为
$R=±UVT（为什么这样？后续证明之）\mathbf{R}=\pm \mathbf{U V}^{T} （为什么这样？后续证明之）$
理论上， $Σ\boldsymbol{\Sigma}$ 的对角线应该非常相近，取均值，求解得到比例系数为
$β=±1/(tr⁡(Σ)/3)\beta=\pm 1 /(\operatorname{tr}(\boldsymbol{\Sigma}) / 3)$
在加上一个限制条件，3D点应该在摄像机的前方
$λ>0:β(xaˉ9+yaˉ10+zaˉ11+aˉ12)>0\lambda>0: \beta\left(x \bar{a}_{9}+y \bar{a}_{10}+z \bar{a}_{11}+\bar{a}_{12}\right)>0$
可确定 $β\beta$ 和 $R\mathbf{R}$ 的 $±\pm$ 符号。接着，可以求得平移向量
$t=β[aˉ4,aˉ8,aˉ12]T\mathbf{t}=\beta\left[\bar{a}_{4}, \bar{a}_{8}, \bar{a}_{12}\right]^{T}$

《视觉14讲》原文：
t矩阵一共有12维，因此最少通过6对匹配的3D-2D特征点即可实现变换矩阵T的线性求解，这种方法就是DLT 直接线性变换法。当匹配点大于6个时，使用SVD分解对超定方程求最小二乘解。如上述步骤所示。

鉴于在DLT求解过程中，我们忽略了R矩阵的正交约束，用DLT求出的结果不一定满足这个约束，是一个一般性的矩阵，平移向量比较好办，它属于三维向量空间。但是旋转矩阵属于SO(3)旋转流形，必须针对 $[R∣t][\mathbf{R} \mid \mathbf{t}]$ 左边3X3的矩阵块，寻找一个最好的旋转矩阵对他进行近似，可以借助QR分解，如下：
$R←(RRT)−12RR\leftarrow(RR^{T})^{-\frac{1}{2}}R$
这就相当于把结果从矩阵空间重新投影到了SE(3)流形上，转换成旋转和平移两部分。

再次说明：通常SLAM问题内参K都是已知的，如果即使未知也可以使用PnP去估计K,R,t三个量。然而由于未知量增多，效果会差一些。

证明的补充：

background:
在ICP 问题中，就业涉及到SVD分解球旋转矩阵的问题，这里也遇到了类似的问题，为什么 $R=±UVT.\mathbf{R}=\pm \mathbf{U V}^{T} .$ 就是最优的?

问题描述之间的刚性转置信息，可以知道这其实是一个最小二乘求优问题，问题可以用如下计算式描述:
$\mathbf{t})=\underset{R, \mathbf{t}}{\operatorname{armgin}} \sum_{i=1}^{n} w_{i}\left\|\left(R \mathbf{p}_{i}+\mathbf{t}\right)-\mathbf{q}_{i}\right\|^{2} \text {, }$
其中 $w_{i}>0$ ，是点集中每个点对的权重。
要求(1)式中的最小值，即为求式中对 $R\mathrm{R}$ 和求导数为 0 的解。

计算位移
将(1)式中的R设为不变量对进行求导，同时令 $F (t) = (R, t)$ ，对 $F (t)$ 求导可得:
$0=∂F∂t=∑i=1n2wi(Rpi+t−qi)=0=\frac{\partial F}{\partial \mathbf{t}}=\sum_{i=1}^{n} 2 w_{i}\left(R \mathbf{p}_{i}+\mathbf{t}-\mathbf{q}_{i}\right)=$

$\mathrm{t}\left(\sum_{i=1}^{n} w_{i}\right)+2 R\left(\sum_{i=1}^{n} w_{i} \mathbf{p}_{i}\right)-2 \sum_{i=1}^{n} w_{i} \mathbf{q}_{i} .$

$p‾=∑i=1nwipi∑i=1nwi\overline{\mathbf{p}}=\frac{\sum_{i=1}^{n} w_{i} \mathbf{p}_{i}}{\sum_{i=1}^{n} w_{i}}$ ,

$q‾=∑i=1nwiqi∑i=1nwi\quad \overline{\mathbf{q}}=\frac{\sum_{i=1}^{n} w_{i} \mathbf{q}_{i}}{\sum_{i=1}^{n} w_{i}}$

$t=q‾−Rp‾\mathbf{t}=\overline{\mathbf{q}}-R \overline{\mathbf{p}}$
在将(4)式代入(1)式可得:
$∑i=1nwi∥(Rpi+t)−qi∥2=∑i=1nwi∥Rpi+q‾−Rp‾−qi∥2==∑i=1nwi∥R(pi−p‾)−(qi−q‾)∥2xi:=pi−p‾,yi:=qi−q‾.——去质心坐标R=argmin⁡R∑i=1nwi∥Rxi−yi∥2\begin{aligned} \sum_{i=1}^{n} w_{i}\left\|\left(R \mathbf{p}_{i}+\mathbf{t}\right)-\mathbf{q}_{i}\right\|^{2} &=\sum_{i=1}^{n} w_{i}\left\|R \mathbf{p}_{i}+\overline{\mathbf{q}}-R \overline{\mathbf{p}}-\mathbf{q}_{i}\right\|^{2}=\\ &=\sum_{i=1}^{n} w_{i}\left\|R\left(\mathbf{p}_{i}-\overline{\mathbf{p}}\right)-\left(\mathbf{q}_{i}-\overline{\mathbf{q}}\right)\right\|^{2} \\ \mathbf{x}_{i}:=\mathbf{p}_{i}-\overline{\mathbf{p}}, \quad \mathbf{y}_{i}:=& \mathbf{q}_{i}-\overline{\mathbf{q}} . —— 去质心坐标\\ R=\underset{R}{\operatorname{argmin}} \sum_{i=1}^{n} w_{i}\left\|R \mathbf{x}_{i}-\mathbf{y}_{i}\right\|^{2} \end{aligned}$
从上可以看出，问题经过转化后变得更加简单，对原来的点集做一个减中心点的预处理，然后再求两个最小二乘的旋转量。

计算旋转量
将(8)式用矩阵表示形式展开，可得:
$∥Rxi−yi∥2=(Rxi−yi)T(Rxi−yi)=(xiTRT−yiT)(Rxi−yi)==xiTRTRxi−yiTRxi−xiTRTyi+yiTyi==xiTxi−yiTRxi−xiTRTyi+yiTyi.\begin{aligned} \left\|R \mathbf{x}_{i}-\mathbf{y}_{i}\right\|^{2} &=\left(R \mathbf{x}_{i}-\mathbf{y}_{i}\right)^{T}\left(R \mathbf{x}_{i}-\mathbf{y}_{i}\right)=\left(\mathbf{x}_{i}^{T} R^{T}-\mathbf{y}_{i}^{T}\right)\left(R \mathbf{x}_{i}-\mathbf{y}_{i}\right)=\\ &=\mathbf{x}_{i}^{T} R^{T} R \mathbf{x}_{i}-\mathbf{y}_{i}^{T} R \mathbf{x}_{i}-\mathbf{x}_{i}^{T} R^{T} \mathbf{y}_{i}+\mathbf{y}_{i}^{T} \mathbf{y}_{i}=\\ &=\mathbf{x}_{i}^{T} \mathbf{x}_{i}-\mathbf{y}_{i}^{T} R \mathbf{x}_{i}-\mathbf{x}_{i}^{T} R^{T} \mathbf{y}_{i}+\mathbf{y}_{i}^{T} \mathbf{y}_{i} . \end{aligned}$
(由于旋转矩阵 $R$ 是正交矩阵，因而有 $R^{\top}=1$ )。同时可以知道上式中 $y⊤Rxx⊤y^{\top} R x x^{\top}$ 和 $i^{\top} R^{\top} y$ 都是标量，而一个标量的转置仍然等于标量本身，因而有:
$xiTRTyi=(xiTRTyi)T=yiTRxi∥Rxi−yi∥2=xiTxi−2yiTRxi+yiTyi\begin{aligned} &\mathbf{x}_{i}^{T} R^{T} \mathbf{y}_{i}=\left(\mathbf{x}_{i}^{T} R^{T} \mathbf{y}_{i}\right)^{T}=\mathbf{y}_{i}^{T} R \mathbf{x}_{i} \\ &\left\|R \mathbf{x}_{i}-\mathbf{y}_{i}\right\|^{2}=\mathbf{x}_{i}^{T} \mathbf{x}_{i}-2 \mathbf{y}_{i}^{T} R \mathbf{x}_{i}+\mathbf{y}_{i}^{T} \mathbf{y}_{i} \end{aligned}$
现在变成要求(11)式的最小值，而该式中只有一项与R有关，其他两项(xi $x i$ i和 $i^{\top} y i$ 都是常量，所以问题转换为求其中一项可变量的最小值，即
$argmin⁡R(−2∑i=1nwiyiTRxi).argmin⁡R(−2∑i=1nwiyiTRxi)=argmax⁡R∑i=1nwiyiTRxi.\begin{aligned} &\underset{R}{\operatorname{argmin}}\left(-2 \sum_{i=1}^{n} w_{i} \mathbf{y}_{i}^{T} R \mathbf{x}_{i}\right) . \\ &\underset{R}{\operatorname{argmin}}\left(-2 \sum_{i=1}^{n} w_{i} \mathbf{y}_{i}^{T} R \mathbf{x}_{i}\right)=\underset{R}{\operatorname{argmax}} \sum_{i=1}^{n} w_{i} \mathbf{y}_{i}^{T} R \mathbf{x}_{i} . \end{aligned}$
$∑i=1nwiyiTRxi=tr⁡(WYTRX)\sum_{i=1}^{n} w_{i} \mathbf{y}_{i}^{T} R \mathbf{x}_{i}=\operatorname{tr}\left(W Y^{T} R X\right)$

上式中的转换是将标量累加转换成矩阵相乘，其中W是 $\times n$ 的对角矩阵，X和Y是 $\times n$ 的矩阵，这些矩阵相乘后的迹就等于等式左边的值。同时，对于矩阵的迹，有如下变换关系:
$tr⁡(AB)=tr⁡(BA)\operatorname{tr}(A B)=\operatorname{tr}(B A)$
$r\left(W Y^{T} R X\right)=\operatorname{tr}\left(\left(W Y^{T}\right)(R X)\right)=\operatorname{tr}\left(R X W Y^{T}\right)$
$S=XXVY⊤,svd⁡(S)==⇒S=UΣVT.\mathrm{S}=X \mathrm{XV} Y^{\top}, \operatorname{svd}(\mathrm{S})==\Rightarrow S=U \Sigma V^{T} .$
$tr⁡(RXWYT)=tr⁡(RS)=tr⁡(RUΣVT)=tr⁡(ΣVTRU)\operatorname{tr}\left(R X W Y^{T}\right)=\operatorname{tr}(R S)=\operatorname{tr}\left(R U \Sigma V^{T}\right)=\operatorname{tr}\left(\Sigma V^{T} R U\right)$
(18)式中最后一步的变换也用到了(15)式的性质。由于 $U 、 R 、 V$ 都是正交矩阵，那么 $M=V⊤RUM=V^{\top} R U$ 也是正交矩阵。
$1=mjTmj=∑i=1dmij2⇒mij≤1⇒∣mij∣<11=\mathbf{m}_{j}^{T} \mathbf{m}_{j}=\sum_{i=1}^{d} m_{i j}^{2} \Rightarrow m_{i j} \leq 1 \Rightarrow\left|m_{i j}\right|<1$
$tr⁡(ΣM)=(σ1σ2⋱σd)(m11m12…m1dm21m22…m2d⋮⋮⋮⋮md1md2…mdd)=∑i=1dσimii≤∑i=1dσi\operatorname{tr}(\Sigma M)=\left(\begin{array}{lllll} \sigma_{1} & & & & \\ & \sigma_{2} & & \\ & & \ddots & \\ & & & \sigma_{d} \end{array}\right)\left(\begin{array}{ccccc} m_{11} & m_{12} & \ldots & m_{1 d} \\ m_{21} & m_{22} & \ldots & m_{2 d} \\ \vdots & \vdots & \vdots & \vdots \\ m_{d 1} & m_{d 2} & \ldots & m_{d d} \end{array}\right)=\sum_{i=1}^{d} \sigma_{i} m_{i i} \leq \sum_{i=1}^{d} \sigma_{i}$
由上述两式可以知道，要求最大迹，就必须使得 $m_{ii}$ 的值等于1，而M又是正交矩阵，那么M就必然是单位矩阵，即有
$I=M=V⊤RU⇒V=RU⇒R=VUTI=M=V^{\top} R U \Rightarrow V=R U \Rightarrow R=V U^{T}$