DLT 算法计算变换矩阵及源码-编程百科-86后生记录生活

DLT 算法计算变换矩阵及源码

2023-09-05 阅读 86 评论 0

摘要：假设原始图像上特征点坐标为 xi=(ui,vi,1)x_i=(u_i,v_i,1)xi=(ui,vi,1)，目标图像上的坐标为xi′=(ui′,vi′,1)x_i'=(u_i',v_i',1)xi′=(ui′,vi′,1) 假设 HHH 为两者之间的变换关系。 Hxi=[h1h2h3h4h5h6h7h8h9]

假设原始图像上特征点坐标为 $x_i=(u_i,v_i,1)$ ，目标图像上的坐标为 $x_i'=(u_i',v_i',1)$
假设 $H$ 为两者之间的变换关系。
$Hxi=[h1h2h3h4h5h6h7h8h9][uivi1]=[h1Txih2Txih3Txi]=[xiTh1xiTh2xiTh3]=[ui′vi′1]Hx_i= \begin{bmatrix} h_1&h_2&h_3\\h_4&h_5&h_6\\h_7&h_8&h_9 \end{bmatrix} \begin{bmatrix} u_i\\v_i\\1 \end{bmatrix} =\begin{bmatrix} h^{1T}x_i\\h^{2T}x_i\\h^{3T}x_i\end{bmatrix}= \begin{bmatrix}x_i^Th^1\\x_i^Th^2\\x_i^Th^3\end{bmatrix}= \begin{bmatrix}u_i'\\v_i'\\1 \end{bmatrix}$

$h_i$ 代表 H 矩阵第 i 行的列向量表示。

可以通过 $xi′⋅xix_i'\cdot x_i$ 得到三个线性方程：

${xiTh3xiTh1=1ui′xiTh3xiTh2=1vi′xiTh2xiTh1=vi′ui′→{vi′xih3−xiTh2=0ui′xiTh3−xiTh1=0ui′xiTh2−vi′xiTh1=0→[03×1T−xiTvi′xiTxiT03×1T−ui′xiT−vi′xiTui′xiT03×1T][h1h2h3]=0\begin{cases} \frac{x_i^Th^3}{x_i^Th_1}=\frac{1}{u_i'}\\ \frac{x_i^Th^3}{x_i^Th_2}=\frac{1}{v_i'}\\ \frac{x_i^Th^2}{x_i^Th_1}=\frac{v_i'}{u_i'} \end{cases} \rightarrow \begin{cases} v_i'x_ih^3-x_i^Th_2=0\\ u_i'x_i^Th_3-x_i^Th_1=0\\ u_i'x_i^Th_2-v_i'x_i^Th_1=0 \end{cases} \rightarrow \begin{bmatrix} 0_{3\times1}^T&-x_i^T&v_i'x_i^T\\x_i^T&0_{3\times1}^T&-u_i'x_i^T\\-v_i'x_i^T&u_i'x_i^T&0_{3\times1}^T \end{bmatrix} \begin{bmatrix} h^1\\h^2\\h^3 \end{bmatrix} =0$

即有 $A_i^{(3)}h=0$ 对于图像片的每一个点。 $A_i$ 是一个 $3×93\times9$ 矩阵，因为 $A$ 的最后一行是由另外两行确定，所以只需要计算线性方程 $A^ih^=0\hat A_i \hat h=0$ 。这里的 $A^i\hat A_i$ 由 $A_i^{(3)}$ 的前两行组成。A 的矩阵表示为：
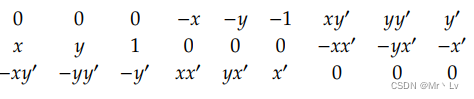
在这里插入图片描述
在估计H时，可以使用更多的匹配点信息来减少估计误差。选取前两行组成一个独立的系数矩阵Ai，将所有的匹配点都考虑在内，形成一个2N × 9的系数矩阵a。用最小二乘法，h的解可以表示为

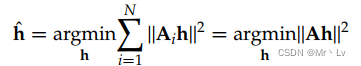
求解上述公式存在两种方式：

奇异值求解
通过SVD 求解 A 的最小右奇异向量作为 h的估计结果。
转化为非齐次线性最小二乘形式。
假设 h9=1，这时等式可以转换为

如果包含n 个匹配点

第一种方式源码如下：

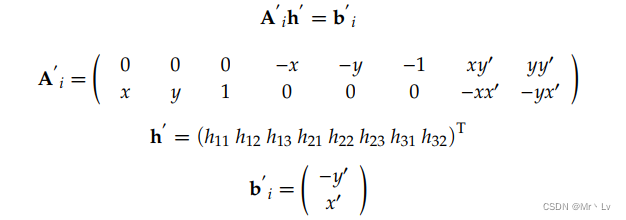
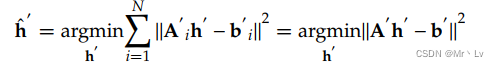
# Ametrix to solv DLTdef matrix_generate(sample_n, cf1, cf2):"""AH=b生成A没对样本能生成一行[[0,0,0,-x,-y,1,xy',yy',y'],[x,y,1,0,0,0,-xx',-yx',-x']]:param sample_n::param cf1: 点1:param cf2::return: A [2N,9]"""A = np.zeros([sample_n * 2, 9], dtype=np.float)for k in range(sample_n):# 每对点对应量A[2 * k, 0] = cf1[k, 0]A[2 * k, 1] = cf1[k, 1]A[2 * k, 2] = 1A[2 * k, 6] = (-cf2[k, 0]) * cf1[k, 0]A[2 * k, 7] = (-cf2[k, 0]) * cf1[k, 1]A[2 * k, 8] = (-cf2[k, 0])A[2 * k + 1, 3] = cf1[k, 0]A[2 * k + 1, 4] = cf1[k, 1]A[2 * k + 1, 5] = 1A[2 * k + 1, 6] = (-cf2[k, 1]) * cf1[k, 0]A[2 * k + 1, 7] = (-cf2[k, 1]) * cf1[k, 1]A[2 * k + 1, 8] = (-cf2[k, 1])return Adef compute_H(src_points,dst_points):A = self.matrix_generate(sample_n, cf1, cf2)# SVD 奇异值求解# Singular Value DecompositionW, U, V = cv2.SVDecomp(A)# get global-homographyh = V[-1, :]h = h.reshape((3, 3))# 反归一化用与还原h = h / h[2, 2]return h

第二种方式，以四组点为例,暂未补充

原文链接：https://808629.com/704.html

发表评论: